图腾柱PFC电路-白日梦想家

本文主要介绍在Boost PFC电路基础上理解图腾柱PFC电路，讨论了图腾柱PFC电路的优势以及控制环路，也简单的介绍了控制过程中涉及到的控制算法（算法会专门出文分析）。

1 回顾单相有源Boost PFC（APFC）变换器基本原理

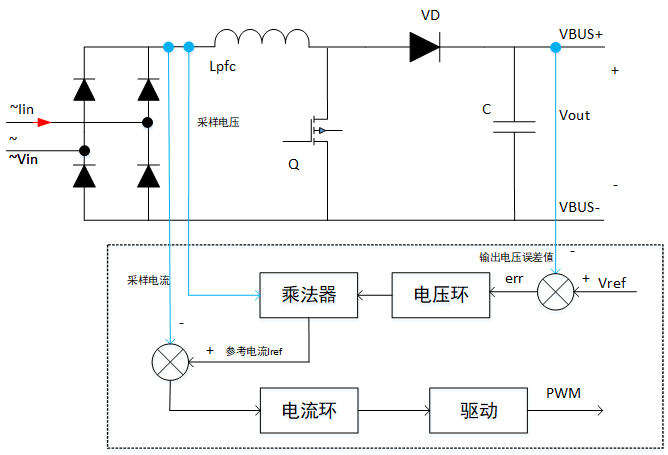
图1 APFC电路控制框图

全桥式整流器直流侧没有直接连接滤波电容，所以后级Boost变换器输入端的电压V_d会在 0V\sim\sqrt{2}V_s，（其中 V_s为电网有效值， \sqrt{2}V_s为电网电压峰值）之间波动。因为Boost型变压器具有升压特性，所以为了使Boost型变换正常工作，输出电压 V_s必须大于输入电压的峰值 \sqrt{2}V_s，即 V_{out}>V_s。

假设输入电网电压有效值 V_s的变化范围为 85V\sim265V,那么输出电压 V_out为：

V_out>\sqrt{2}V_{smax}=\sqrt{2}\times265V\approx 374V \tag{1}

通常选择输出电压 V_o为400V或者390V。在单相Boost型PFC变换器中根据电感的伏秒平衡原理，可得：

DT_{sw}v_{in}(t)=(1-D)T_{sw}(v_o-v_{in}) \tag{2}

其中 v_{in}(t)=\sqrt{2}V_ssin(wt)为交流输入电压表达式，经计算得：

D=1-\frac{V_s}{v_o}sin(wt) \tag{3}

根据式子来看，APFC变换器的基本原理就是，通过控制有源器件的占空比随输入电压呈正弦变化，使得输入电流正弦化，同时输入电流相位跟踪输入电压。如下图为平均电流控制的APFC变换器电感电流波形。

2 基本无桥PFC变换器案例分析

针对传统APFC变换器中整流堆二极管通态损耗问题而提出的方案——基本型无桥PFC变换器，如下图所示。与APFC变换器对比，APFC变换电路电流通路路经上有三个半导体器件，而基本型无桥变换器在电流通路路径上只有两个半导体器件。但是MOS管和快速二极管多了一倍（成本增加了），同时控制上相对复杂（相较于APFC），而且EMC(电磁兼容)、EMI(电磁干扰)要额外处理（Q2管子在负半周期时两端电压一直以开关频率在 0V\sim V_{bus}跳变，寄生电容将高频跳变的电压信号耦合到输入侧。所以该拓扑适合应用在对效率要求较高的场景下。

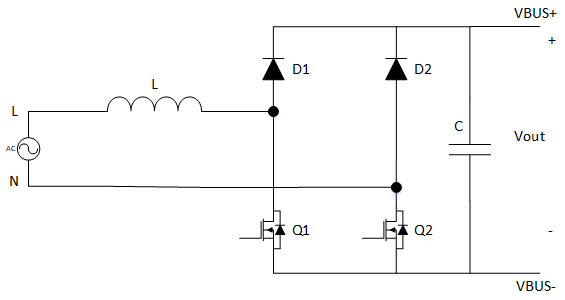
图2 基本型无桥PFC变换器拓扑结构图

分析基本型无桥Boost PFC变换器的稳态特性：对于交流输入的正负半周期而言，基本型无桥Boost PFC可以等效为两个电源电压相反的Boost PFC电路的组合(如下图所示)。

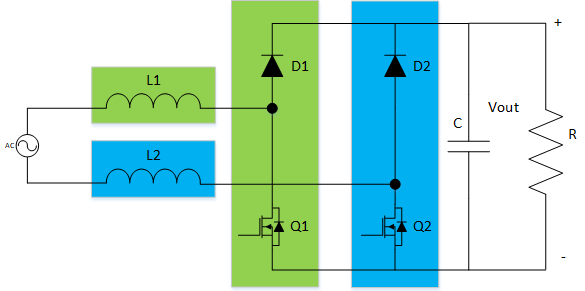
图3 基本型无桥PFC变换器等效拓扑结构图

在输入电压为正半周期内，电感电流为正，在这个阶段有两个工作模态（Q1为PWM工作状态）：

模态1：支路1的MOS管Q1处于PWM工作状态，同时支路2的MOS管Q2续流(可以通过体二极管续流也可以通过MOS续流，取决于控制方式)，为电感L1、L2储能。负载由电容供能。
模态2：支路1的二极管D1导通，同时支路2的MOS管Q2续流，负载由电感L1、L2以及供电电源同为负载供能，电感储能减少。

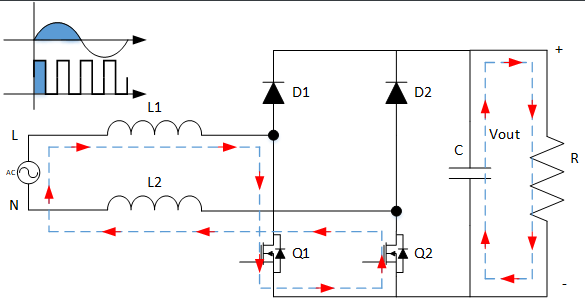
图4 基本型无桥PFC变换器工作模态1

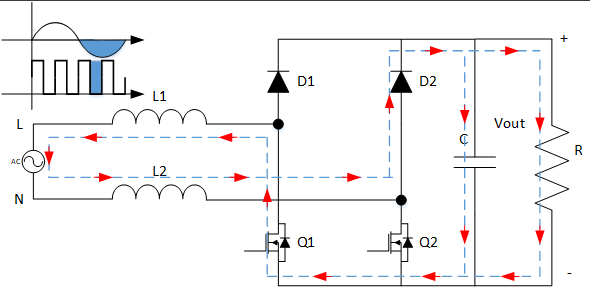
图5 基本型无桥PFC变换器工作模态2

	表1 传统APFC与基本无桥PFC所用器件对比
	整流二极管	MOS管	快恢复二极管	导通	关断
传统APFC	4	1	1	2个整流二极管 1个MOS管	2个整流二极管 1个快恢复二极管
基本无桥PFC	0	2	2	1个体二极管或MOS管 1个MOS管	1个体二极管或MOS管 1个快恢复二极管

表1 传统APFC与基本无桥PFC所用器件对比

整流二极管

MOS管

快恢复二极管

导通

关断

传统APFC

2个整流二极管

1个MOS管

2个整流二极管

1个快恢复二极管

基本无桥PFC

1个体二极管或MOS管

1个MOS管

1个体二极管或MOS管

1个快恢复二极管

3 图腾柱无桥PFC变换器分析

3.1 PFC电路工作模式

Boost型PFC变换器依据电感电流是否连续分为三种模式：电流连续模式(CCM)、电流临界模式(CRM)和电流断续模式(DCM)。如下图为三种模式下电感电流波形图。

连续电流模式（Continuous Current Mode，CCM）：在一个开关周期内，电感上始终有电流流过，且电流不会到零。
断续电流模式（Discontinuous Current Mode，DCM）：在一个开关周期内，电感电流会存在一段时间为零的状态。
临界导通模式（Critical Conduction Mode，CRM）：处于CCM模式和DCM模式之间，其电感电流会在周期末刚好减小到零，然后进入下一个开关周期。

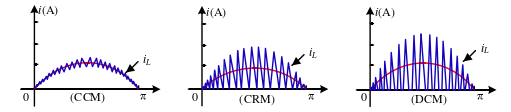
图6 三种模式下电感电流波形图

三种模式的优缺点：

基于CCM模式的电流控制是目前应用最广泛的双闭环控制方式。优点在于电感电流纹波小，流过器件的电流有效值小，器件所受的电流应力小，且功率因数较高，所以CCM模式通常应用于中大功率场合；缺点是它在使用模拟控制时要使用乘法器，控制电路和采样电路的设计相对复杂，在三种模式中电感值较大，不利于体积的缩小，另外使用硬开关模式，开关损耗也比较大。
CRM模式可以看做是连续导通模式的特殊情况，优点在于开关管可以实现零电流关断（ZCS），输入电流功率因数较高，电感值较小；缺点是在CRM模式下存在开关频率在工频周期内变化的问题，滤波电路比较难设计，且电感电流纹波比较大，一般适用于中小功率场合。
DCM模式可以实现开关管的零电流开通，通常它的控制电路比较简单，且采样电路没有CCM模式负载，但是该模式下电感电流的文博最大，输入EMI和开关管上的电流应力较大，通常应用在小功率场合。

3.2 CCM模式下图腾柱无桥PFC变换器分析

采用Si MOSFET作为开关管时，其自身的寄生体二极管存在严重的反向恢复问题，使得电路在较大功率等级下无法工作在CCM模式，只能工作在DCM或CRM模式，其实图腾柱无桥PFC很早就被提出来了，但应用却不广泛。

3.2.1 CCM模式下电路工作模态分析

图腾柱无桥PFC电路拓扑如下图所示，GaN功率开关管 S_1和 S_2作为高频管构成图腾柱结构，在该结构下 S_1和 S_2的PWM驱动信号是互补的。低频管 S_3和 S_4作为续流管使用，通常选用普通MOSFET就可以。

根据输入电压半个周期情况，一次只有一个开关管接通， V_{ac}是交流电压源输入，L是Boost升压电感，C为母线滤波电容，R为输出负载。

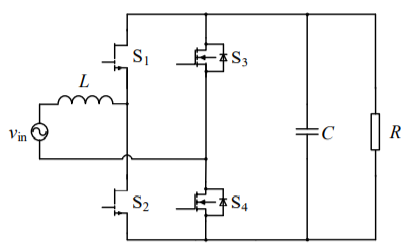
图7 图腾柱无桥PFC电路拓扑图

当交流输入为正半周期时， S_4始终处于开通状态， S_3始终处于关断状态，此时可以分成两个工作模态：

模态1： S_2导通，输入电压经过 L、S_2、S_4形成回路，给电感L供电储能，电感电流线性上升。与此同时母线电容C对负载放电，以维持输出稳定。如图(a)所示。
模态2： S_2关断时， S_1作为续流管导通，交流输入和电感同时给母线电容以及负载供电，电感电流下降，如图(b)所示。

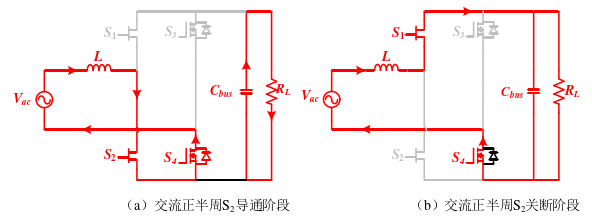
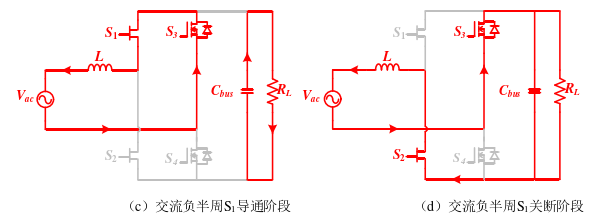
当交流输入为负半周期时，与正半周期相反， S_3始终处于开通状态， S_4始终处于关断状态，同样可以分成两个工作模态：

模态3： S_1导通，输入电压经过 L、S_1、S_3形成回路，给电感L供电储能，电感电流线性上升。与此同时母线电容C对负载放电，以维持输出稳定。如图(c)所示。

模态4： S_1关断时， S_2作为续流管导通时，交流输入和电感同时给母线电容以及负载供电，电感电流下降。如图(d)所示。

3.2.2 功率电路模型分析(待补充！！！)

4 控制策略分析

4.1 静态坐标系下系统控制策略分析

4.1.1 CCM模式下的控制方式

当图腾柱无桥PFC变换器工作在CCM模式下，可以直接对电感电流进行控制，常见的控制方法有峰值电流模式控制（Peak Current Mode，PCM）控制、平均电流模式（Average Current Mode，ACM）控制以及滞环电流模式（Hysteretic Current Mode，HCM）控制。

1）峰值电流模式控制

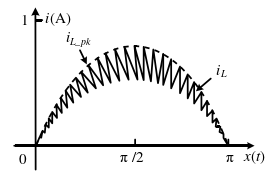
图8 电感电流峰值包络线 i_L(pk)跟踪输入电压 V_{ac}

峰值电流控制是通过直接控制电感电流 i_L，使其峰值包络线跟踪输入电压 V_{ac}的波形，从而使输入电流与输入电压同等相位，并维持较好的正弦度。如图8所示为采用峰值电流控制时电感电流 i_L波形，虚线表示的是各个开关周期内电感电流峰值的包络线。峰值电流控制比较灵活，有瞬时过流保护的能力，但是在占空比大于0.5时会产生次谐波震荡，所以在有源PFC控制策略中不常用。

2）平均电流模式控制

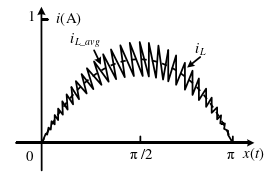
图9 电感电流平均值 i_L(avg)跟踪输入电压 V_{ac}

平均电流模式控制是当前有源PFC电路中应用最多的一种控制方法，平均电流控制使基准信号 I_{ref}与输入电压保持同相位，对单个开关周期内的电感电流平均值进行控制，以此进行功率因数矫正，采用平均电流控制方法电感电流波形如上图所示。由于平均电流控制需要较高增益带宽的电流环，以对高频误差信号进行追踪，所以平均电流控制下输入电流的PF值较高，且不易受到电路中高频信号的干扰。故在实际中得到广泛应用。

3）滞环电流模式控制（不做分析）

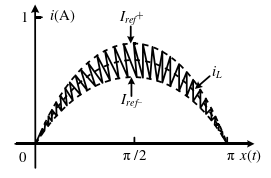
图10 电感电流 i_L跟踪电流参考信号 I_{ref}^+和 I_{ref}^-构成的滞环带

滞环电流模式控制将电感电流信号与两个参考信号 I_{ref}^+和 I_{ref}^-作比较，两个参考信号组成一个滞环带，以此实现对开关器件的控制，用滞环电流模式控制法控制的电感电流波形如上图所示。滞环电流模式控制具有控制简单，电流动态响应快，有内在电流限制能力，但是滞环电流控制模式的控制频率是变化的，受负载影响大，滤波器设计需要参考最低频率情况，实际设计中变换器通常无法达到更优。

4.1.2 峰值电流模式控制下的双环策略

图12为图腾柱无桥PFC变换器基于峰值电流控制框图。 V_{oref}为输出电压参考值，输出电压 V_{o}在电压外环的控制下跟踪到 V_{oref}。当定频脉冲信号Clock上升沿到来时，主开关导通（在输入电压正半周期， S_2作为主开关， S_1作为续流导通， S_4始终导通；在输入电压负半周期， S_1作为主开关， S_2作为续流导通， S_3始终导通）。当电感电流上升到电感电流给定参考值时，主开关关闭。电感电流给定参考值由电压外环控制器输出 v_e、锁相环输出和斜坡补偿电压 v_p组成。因此，电感电流与输入电压实现同步，从而获得单位功率因数。

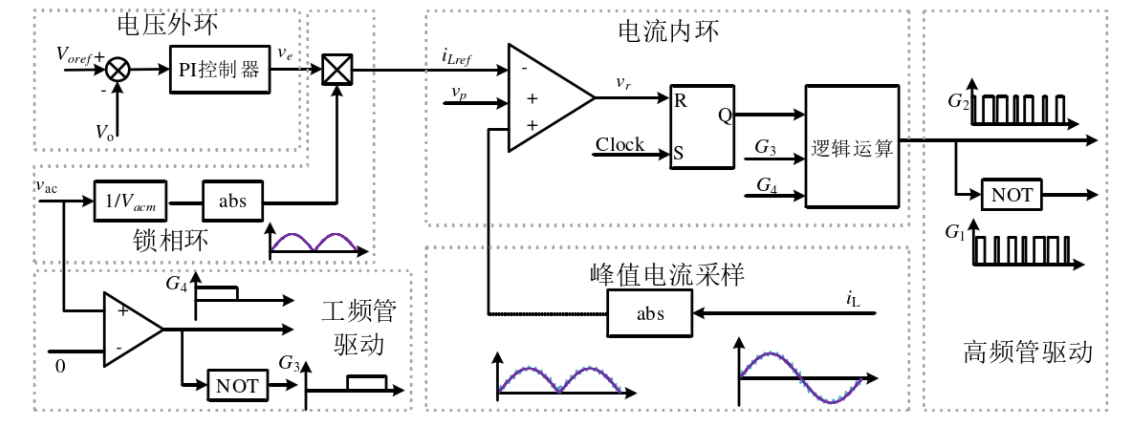
图11 图腾柱无桥PFC变换器基于峰值电流控制的控制框图

峰值电流控制工作在定开关频率，不需要额外的电流控制器，避免对电流控制器参数的设计，电流峰值参考值的设定在一定程度上起到了限流的作用。但是峰值电流控制有许多不足：

当主开关占空比大于0.5时，存在次谐波振荡，需要加入斜坡补偿电压，如图12所示为连续模式下电感电流波形图，在kT_s时刻，电感电流在谷值时收到扰动 \Delta i_L(k)，i_{Lval1}(k)为 kT_s时刻受到扰动是的电感电流谷值电流， i_{Lval}(k)为 kT_s时刻未受到扰动时的电感电流谷值电流，D'为受到扰动时的主开关的占空比，D为未受到扰动时的主开关的占空比。蓝色线为电感电流给定参考值，红色线为受到扰动时的电感电流波形，黑色为未受到扰动时的电感电流波形。

\Delta i_L(k)=i_{Lval}(k)-i_{Lval1}(k) \tag{4}

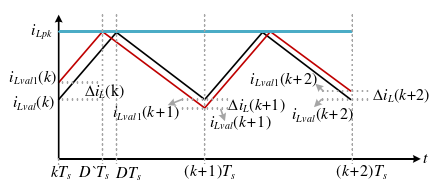
图12 连续模式电感电流波形图

在 (k+1)T_s时刻，电感电流受到扰动和未受到扰动时的谷值电流如下所示：

\Delta i_{Lval1}(k+1)=i_{Lpk}-\frac{T_s(1-D^{'})(V_o-V_{ac})}{L} \tag{5}

\Delta i_{Lval}(k+1)=i_{Lpk}-\frac{T_s(1-D)(V_o-V_{ac})}{L} \tag{6}

结合式(4)、(5)、(6)得到 \Delta i_L (k+1):

\Delta i_L(k+1)=-\frac{D}{1-D}\Delta i_L(k) \tag{7}

在 (k+2)T_s时刻， \Delta i_L(k+2)如下所示：

\Delta i_L(k+2)=(\frac{D}{1-D})^2\Delta i_L(k) \tag{8}

电感电流扰动在经过两个开关周期后相位一致，扰动频率为开关周期的一半，所以称该扰动为次谐波。当占空比小于0.5时，电感电流扰动减小；当占空比大于0.5时，电感电流扰动增大存在次谐波扰动。

在输入电压升高和轻载工况下，由于斜坡补偿电压的存在，电感电流存在严重的失真现象。
控制系统对噪声的敏感度高。电感电流峰值电流的采样容易收到噪声的干扰，带入电流内环控制的噪声引起电感电流波形的失真。

4.1.3 平均电流模式控制下的双环策略

图13为图腾柱无桥PFC变换器基于平均电流控制框图。电压外环通过对输出电压的闭环反馈，获得稳定的输出电压，输出电流为直流量，PI控制器可以实现输出电压零稳态误差。PI控制器的输出决定了电流给定参考值的幅值，负载的变化引起PI控制器输出的变化，满足功率守恒。电流给定参考值为电压外环控制器输出与锁相环输出的乘积。锁相环的输出反映了输入电压相位的变化。电流内环采用准PR控制器可以实现电感电流零稳态误差。准PR控制器的输出通过SPWM调制技术得到高频管驱动。工频管驱动取决于输入电压过零点变化。

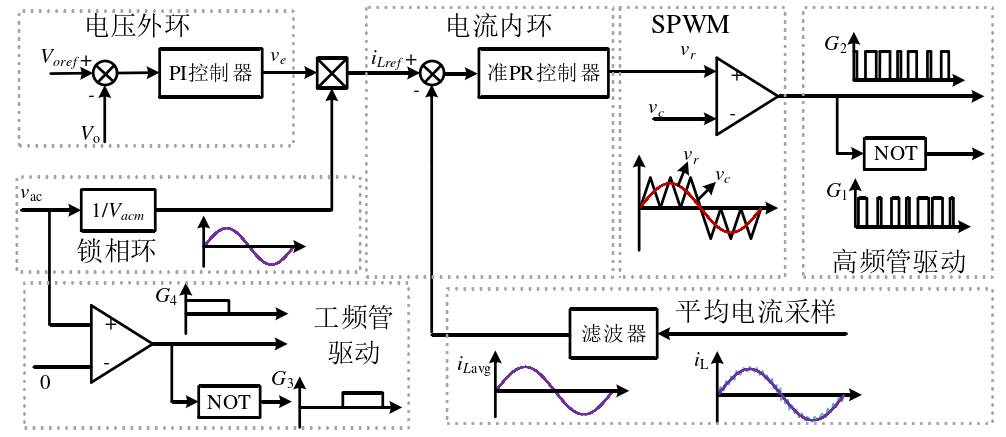
图13 图腾柱无桥PFC变换器基于平均电流控制框图

开关次谐波对电流内环的影响很重要，为了获得每个开关周期里电流采样的平均值，需对其开关次谐波进行滤波。平均电流有如下优势：

更好的抗噪声干扰能力。峰值电流控制需要得到电感电流峰值电流信息，在电流峰值处开关动作，由于电路寄生电容和杂散电感的存在，容易引起电感电流的振荡，从而引起开关的误动作。平均电流控制需要得到每个开关周期里的平均电流，通过加入电流采样滤波器对电流噪声进行抑制，从而得到光滑的电感电流波形。
电流采样频率大大降低。峰值电流控制为了得到电流峰值信息，需要高电流采样频率，采样频率一般为开关频率的几十倍以上，数字控制难以实现，往往采用模拟控制。平均电流控制在每个开周期里只需采样一次，采样频率一般为开关频率，也可以低于开关频率，但是会使得工频次谐波更大。因此，电流平均控制可以方便通过数字控制实现。
不需要斜坡补偿。峰值电流控制在占空比大于0.5时，为防止谐波振荡，需要加入斜坡补偿器。

4.1.4 平均电流模式控制系统参数设计及稳定性分析

如图14所示为频域下基于平均电流控制的信号简化控制框图。 G_v(s)为PI控制器传递函数，其中 k_{p1}为比例环节系数， k_i为积分环节系数。 G_i(s)为准PR控制器传递函数，其中 k_{p2}为比例环节系数， k_r为谐振环节系数， w_c为阻尼频率， w_0为谐振频率。

G_v(s)=k_{p1}+\frac{k_i}{s} \tag{9}

G_i(s)=k_{p2}+\frac{2k_rw_cs}{s^2+2w_cs+w_0^2} \tag{10}

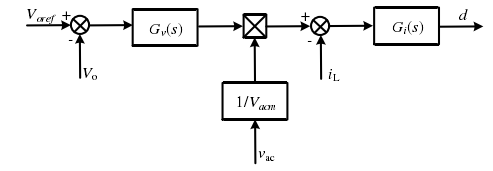
图14 频域下基于平均电流控制的信号简化控制框图

根据图14可以得到占空比d的表达式，如下式：

d=[(V_{oref}-V_o)G_v(s)\frac{v_{ac}}{V_{acm}}-\hat{i}_L]G_i(s) \tag{11}

所以控制系统的小信号表达式，如下式：

\hat{d}=[(\hat{v}_{oref}-\hat{v}_o)G_v(s)\frac{v_{ac}}{V_{acm}}-\hat{i}_L]G_i(s) \tag{12}

根据上式容易的到系统小信号框图如下所示：

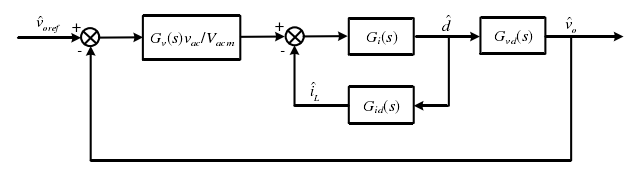
图15 系统小信号框图

电流内环开环传递函数 G_{io}(s)如下式所示：

G_{io}(s)=G_{id}(s)G_i(s)=\frac{sC_oV_o+(1-D)i_L+\frac{V_o}{R}}{LC_os^2+\frac{L}{R}s+(1-D)^2}(k_{p2}+\frac{2k_rw_cs}{s^2+2w_cs+w_o^2}) \tag{13}

在稳态情况下电网输入电压为：

v_{ac}=V_{acm}sin(w_gt) \tag{14}

其中 w_g为电网电压角频率， V_{acm}为峰值电压

由充放电平衡得到输入电压 v_{ac}、输出电压 V_o以及主开关 T_2占空比D的关系式：

(1-D)V_o=v_{ac} \tag{15}

不考虑功率损耗，有输入输出功率守恒可得到输入电流 i_L、输入电压 v_ac、输出电压 V_o和负载R的关系式：

i_L=\frac{2V_o^2}{RV_{acm}^2}v_{ac}\tag{16}

将式 (14)、(15)、(16)代入 (13)化简得：

G_{io}(s)=\frac{V_oC_os+\frac{2V_ov_{ac}^2}{RV_{acm}^2}+\frac{V_o}{R}}{LC_os^2+\frac{L}{R}s+\frac{v_{ac}^2}{V_o^2}}(k_{p2}+\frac{2k_rw_cs}{s^2+2w_cs+w_0^2})\tag{17}

假设准PR控制器谐振系数 k_r=0，比例系数 k_{p2}=1，电流内环闭环传递函数为 G_{io}(s)。

G_{il}(s)=\frac{1}{1+G_{io}(s)} \tag{18}

闭环传递函数的特征根方程如下式所示：

D(s)=LC_os^2+(\frac{L}{R}+V_oC_o)s+\frac{v_{ac}^2}{V_o^2}+\frac{2V_ov_{ac}^2}{RV_{acm}^2}+\frac{V_o}{R}=0 \tag{19}

其特征根方程有两个极点 p_1、p_2，如下所示：

p_1=-a+\sqrt{a^2-b}\\ p_2=-1-\sqrt{a^2-b} \tag{20}

其中a和b如下所示：

a=\frac{1}{2LC}(\frac{L}{R}+V_oC_o)\\ b=\frac{1}{LC_o}(\frac{v_{ac}^2}{V_o^2}+\frac{2V_ov_{ac}^2}{RV_{acm}^2}+\frac{V_o}{R}) \tag{21}

假设输入电压有效值、输出电压、输入电感、输出电容、输出负载参数如下表所示：

参数	值
输入电压有效值 V_{acrms}	110V
输出电压 V_o	350V
输入电感L	2mH
输出电容 C_o	470uF
负载R	122.5Ω

将参数带入（21）式的a，b中，则 a^2>>b，即电流内环闭环传递函数的两个特征根落在负半周平面上，故而在比例控制器时，只要比力系数大于0，即可使电流内环稳定。

4.1.5 CCM模式下电路参数设计

名称	符号/单位	参数
电网输入电压RMS	V_{acrms}/V	185~265
最大输出功率	P_o/W	410
母线输出电压	V_o/V	390~410
变换器效率	η/\%	≥98
功率因数	PF	0.99
输入电流谐波	THD/\%	≤5%
开关频率	f_s/KHz	200

4.1.5.1 升压电感设计

最大输入电流的有效值为：

I_{inRMSmax}=\frac{P_{omax}}{\eta V_{inRMSmin}}=\frac{410}{0.98\times 185}=2.261A \tag{22}

I_{inRMSmax}为最大输入电流的有效值， P_{omax}为最大输出功率， \eta为变换器的效率， V_{inRMSmin}为输入电压有效值的最小值。

则输入电流的峰值为：

I_{inpk}=\sqrt{2}*I_{inRMSmax}=3.198A \tag{23}

通常，假设纹波率设为20%左右，求得升压电感上最大纹波电流为：

\Delta I_{L_{max}}=0.2\times I_{in_pk}=0.64A \tag{24}

升压电感电流峰值为：

I_{L_{pk(max)}}=I_{inpk}+\frac{\Delta IL_{max}}{2}=3.52A \tag{25}

在输入电压最小是，占空比D为：

D=\frac{V_o-\sqrt{2}V_{inRMSmin}}{V_o}=\frac{410-\sqrt{2}\times 185}{410}=0.362 \tag{26}

其中，$V_o$为母线输出电压。

则升压电感的电感量L为：

L=\frac{\sqrt{2}V_{inRMSmin}D}{\Delta I_{L_{max}f_s}}=\frac{\sqrt{2}\times 185 \times 0.362}{0.64\times 200000}=740uH \tag{27}

选取电感值为800uH的电感作为升压电感。

4.1.5.2 母线输出电容设计

对于图腾柱无桥PFC变换器，要考虑直流侧的掉电维持时间和母线电压纹波，通常掉电维持时间去一个工频周期时间，即20ms，输出电容值计算如下所示：

C_o=\frac{2P_ot_{hold}}{V_o^2-V_{omin}^2} \tag{28}

其中， P_o为满载输出功率， V_{omin}为输出电压最小值。

在实际选取时，取母线电压纹波小于 5\%，取 V_{omin}的值为360V，代入上式可以计算的电容危 425uF，考虑留有余量选取 470uF的电解电容作为输出电容。

与此同时，主开关管工作在高频开关状态下，会带来一定的电压纹波。因此通常会在大的电解电容上并联一些小电容阻止高频纹波对负载带来的影响，以一个开关周期为例，当主开关关断后，流进续流管的电流可以表示为：

i_{fw}=\frac{t_{off}}{T}I_{in}sinwt=\frac{\sqrt{2}V_{in}sinwt}{V_o}I_{in}sinwt=\frac{\sqrt{2}V_{in}}{2V_o}I_{in}-\frac{\sqrt{2}V_{in}}{2V_o}I_{in}cos2wt \tag{29}

由上式可知，流进续流管的电流由两部分组成，一部分是母线电流，另外一部分为二倍频的纹波电流，所以，需要被吸收的电流为：

i_c=\frac{\sqrt{2}V_{in}}{2V_o}I_{in}cos2wt \tag{30}

根据公式推得纹波电压为：

\Delta v\geq\frac{P_o}{2wCV_o\eta} \tag{31}

计算的高频电容大小为：

C\geq\frac{P_o}{2\Delta v\eta wV_o}=\frac{410}{2\times 10\times 0.98\times 2\times \pi \times 200000 \times 410}=40.6nF \tag{32}

目录CONTENT

图腾柱PFC电路